二叉排序树｜Binary Sort Tree

本文最后更新于：June 1, 2023 9:58 PM

这是在看b站上的韩顺平老师的数据结构与算法[1]时做的笔记。等我把后面的都更新完了以后会陆续把前面的补上。

一、实际案例

给你一个数列（7，3，10，12，5，1，9）要求能够高效地完成对数组的查找与添加

二、解决方案

  • 使用数组｜ArrayList
    1. 数组未排序时：
      • 优点：直接在尾部添加，速度快
      • 缺点：查找速度慢
    2. 数组排序时：
      • 优点：用二分查找时，查找速度快
      • 缺点 ：为了保证数组有序，添加新数据时速度慢
  • 链式存储-链表｜LinkedList
    • 优点：添加数据速度比数组快，因为不需要整体移动
    • 缺点：查找速度慢
  • 二叉排序树｜BST
    • 增删改查效率都比较高

三、基本介绍

一个很好用的BST的可视化网站

二叉排序树：BST(Binary Sort(Search) Tree)， 对于它的任何一个非叶子结点｜leaf node，要求左子结点的值比当前结点的值小，有子结点的值比当前结点的值大。

特别说明：如有相同的值，可以将该结点放在左子结点或右子结点（最好避免相同的值）

四、构建BST

针对前面的数据（7，3，10，12，5，1，9），对应的二叉排序树为：

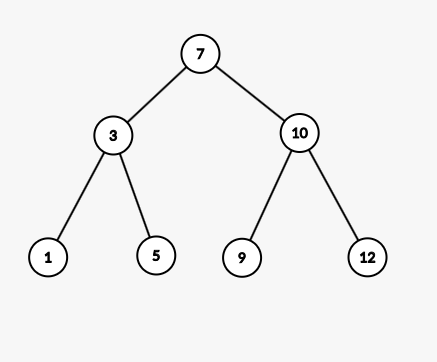
![](https://gitee.com/Trotyl15/blogImage/raw/master/img/note/d&a/BST.png)

当插入结点“2”时，“2”应该放在“1”的右子结点

五、删除结点的思路

第一种情况

——删除叶子结点（如：1，5，9，12）

1） 定位结点 targetNode

2）找到targetNode的父结点 parent

3）确定targetNode是parent的左子结点还是右子结点

4）根据前面的情况对应删除

左子结点：parent.left = null;

右子结点：parent.right = =null;

第二种情况

——删除只有一颗子树的结点（如：3）

1） 定位结点 targetNode

2）找到targetNode的父结点 parent

3）确定targetNode的子结点是左结点还是右子结点

  • 如果targetNode有左子结点
    1. targetNode是parent的左子结点
      parent.left = targetNode.left ;
    2. targetNode是parent的右子结点
      parent.right = targetNode.left ;
  • 如果targetNode有右子结点
    1. targetNode是parent的左子结点
      parent.left = targetNode.right ;
    2. targetNode是parent的右子结点
      parent.right = targetNode.right ;

第三种情况

——删除有两颗子树的结点（如：7，3，10）

  • 这里用“10”举例，并且假设“12”下面还有两个子结点

1） 定位结点 targetNode

2）找到targetNode的父结点 parent

3）从targetNode的右子树找到最小的结点

4）用一个临时变量，将右子树最小的结点值保存 temp = 11

5）删除该最小结点

6）targetNode.value = temp;

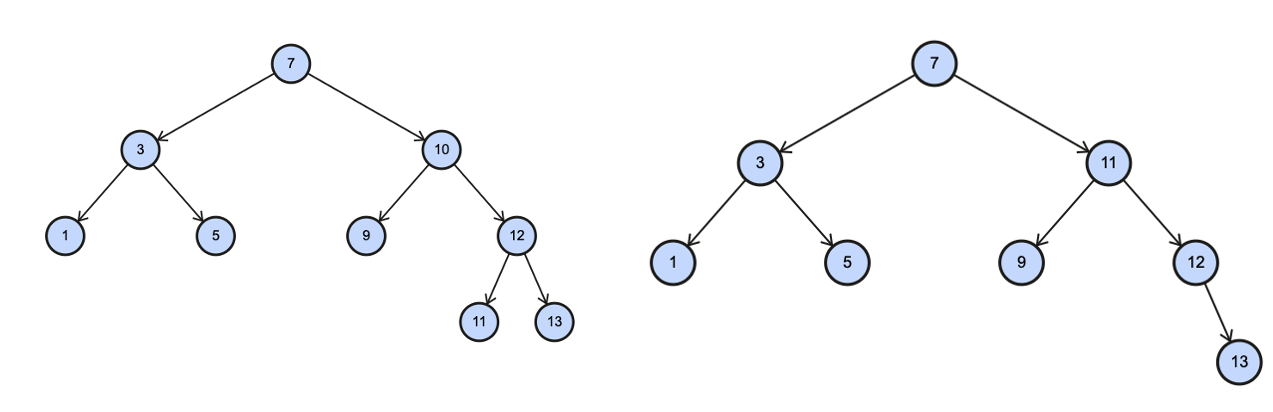
容我说一句：妙啊！

六、代码实现

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
public class BinarySortTreeDemo {
    public static void main(String[] args) {
        int[] arr = { 7, 3, 10, 12, 5, 1, 9, 2 };
        BinarySortTree binarySortTree = new BinarySortTree();
        for (int i = 0; i < arr.length; i++) {
            binarySortTree.add(new Node(arr[i]));
        }
        binarySortTree.infixOrder();// 1, 2, 3, 5, 7, 9, 10, 12
		binarySortTree.delNode(2);
		binarySortTree.delNode(5);
		binarySortTree.delNode(9);
		binarySortTree.delNode(12);
		binarySortTree.delNode(7);
		binarySortTree.delNode(3);
		binarySortTree.delNode(10);
		System.out.println("After:");
		binarySortTree.infixOrder();
    }
}

// 创建树
class BinarySortTree {
    private Node root;

    public Node search(int value) {
        if (root == null) {
            return null;
        } else {
            return root.search(value);
        }
    }

    public Node searchParent(int value) {
        if (root == null) {
            return null;
        } else {
            return root.searchParent(value);
        }
    }

    public int delRightTreeMin(Node node) {
        Node target = node;
        while (target.left != null) {
            target = target.left;
        }

        delNode(target.value);
        return target.value;
    }

    public void delNode(int value) {
        if (root == null) {
            return;
        } else {
            Node targetNode = search(value);
            if (targetNode == null) {
                return;
            }
            if (root.left == null && root.right == null) {
                root = null;
                return;
            }
            Node parent = searchParent(value);
            if (targetNode.left == null && targetNode.right == null) {
                if (parent.left != null && parent.left.value == value) {
                    parent.left = null;
                } else if (parent.right != null && parent.right.value == value) {
                    parent.right = null;
                }
            } else if (targetNode.left != null && targetNode.right != null) {
                int minVal = delRightTreeMin(targetNode.right);
                targetNode.value = minVal;
            } else {
                if (targetNode.left != null) {
                    if (parent != null) {
                        if (parent.left.value == value) {
                            parent.left = targetNode.left;
                        } else {
                            parent.right = targetNode.left;
                        }
                    } else {
                        root = targetNode.left;
                    }
                } else {
                    if (parent != null) {
                        if (parent.left.value == value) {
                            parent.left = targetNode.right;
                        } else {
                            parent.right = targetNode.right;
                        }
                    } else {
                        root = targetNode.right;
                    }
                }
            }
        }
    }

    public void add(Node node) {
        if (root == null) {// 如果是空树，直接让root指向node
            root = node;
        } else {
            root.add(node);
        }
    }

    // 中序遍历
    public void infixOrder() {
        if (root != null) {
            root.infixOrder();
        } else {
            System.out.println("Tree is Empty.");
        }
    }
}

// 创建Node节点
class Node {
    int value;
    Node left;
    Node right;

    public Node(int value) {
        this.value = value;
    }

    /**
     * 
     * @param value 希望删除的值
     * @return 如果找到返回该结点，否则返回null
     */
    public Node search(int value) {
        if (value == this.value) {
            return this;
        } else if (value < this.value) {
            if (this.left == null) {
                return null;
            }
            return this.left.search(value);
        } else {
            if (this.right == null) {
                return null;
            }
            return this.right.search(value);
        }
    }

    public Node searchParent(int value) {
        if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
            return this;
        } else {
            if (value < this.value && this.left != null) {
                return this.left.searchParent(value);
            } else if (value >= this.value && this.right != null) {
                return this.right.searchParent(value);
            } else {
                return null;
            }
        }

    }

    @Override
    public String toString() {
        return "Node [value=" + value + "]";
    }

    // 添加节点
    public void add(Node node) {
        if (node == null) {
            return;
        }
        if (node.value < this.value) {
            if (this.left == null) {
                this.left = node;
            } else {
                this.left.add(node);// 递归
            }
        } else {
            if (this.right == null) {
                this.right = node;
            } else {
                this.right.add(node);// 递归
            }
        }
    }

    // 中序遍历
    public void infixOrder() {
        if (this.left != null) {
            this.left.infixOrder();
        }
        System.out.println(this);
        if (this.right != null) {
            this.right.infixOrder();
        }
    }
}

运行结果

1
2
3
4
5
6
7
8
9
10
Node [value=1]
Node [value=2]
Node [value=3]
Node [value=5]
Node [value=7]
Node [value=9]
Node [value=10]
Node [value=12]
After:
Node [value=1]

参考

  1. 尚硅谷Java数据结构与java算法，韩顺平数据结构与算法 ↩