平衡二叉树｜AVL Tree

本文最后更新于：July 27, 2024 8:58 PM

这是在看b站上的韩顺平老师的数据结构与算法[1]时做的笔记。等我把后面的都更新完了以后会陆续把前面的补上。

一、实际案例

给你一个数列 {1, 2, 3, 4, 5, 6}，要求创建一颗二叉排序树（BST），并分析问题所在。

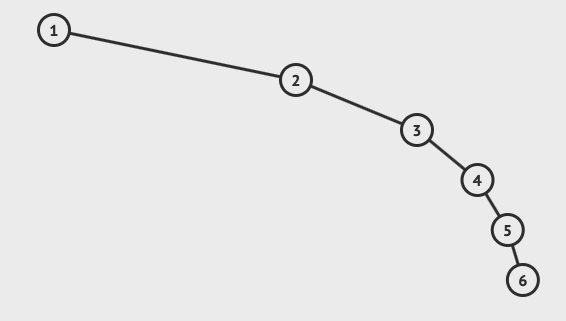
问题分析：

  1. 左子树全部为空，从形式上看，更像一个单链表
  2. 插入速度没有影响
  3. 查询速度明显降低（因为需要依次比较），不能发挥BST的优势，因为每次还需要比较左子树，其查询速度比单链表还慢
  4. 解决方案-平衡二叉树（AVL）

二、基本介绍

平衡二叉树又称平衡二叉搜索树（Self-balancing binary search tree），是二叉排序树的一类，又被称为AVL树，可以保持查询效率比较高。

具有一下特点：它是一颗空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一颗平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL（算法，不是指AVL树）、替罪羊树、Treap、伸展树等。


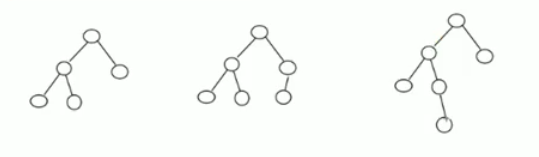
上面的三个树只有左边两个是AVL树。

三、应用案例

1. 单旋转—左旋转

1）要求

给你一个数列，创建出对应的平衡二叉树 {4, 3, 6, 5, 7, 8}

2）思路

问题：

当插入“8”时rightHeight()-leftHeight()>1成立，此时，不再是一颗AVL树了

处理过程-进行左旋转：

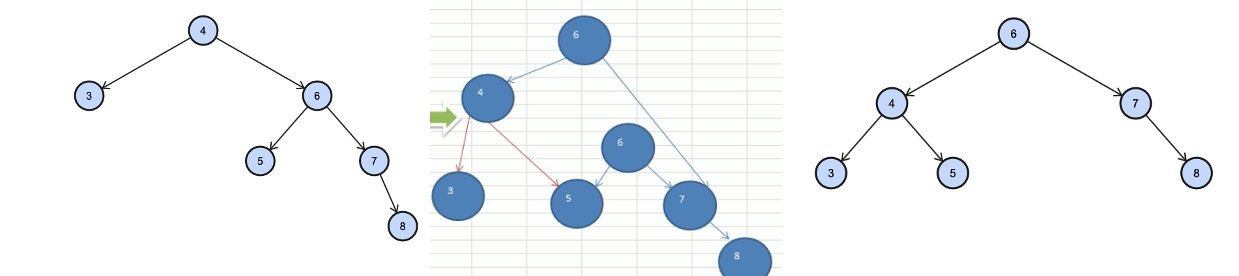
  1. 创建新的结点，以当前根结点的值

Node newNode = new Node(value);

  1. 把新的结点的左子树设置成当前结点的左子树

newNode.left = left;

  1. 把新的结点的右子树设置成带你过去结点的右子树的左子树

newNode.right = right.left;

  1. 把当前结点的值替换成右子结点的值

value = right.value;

  1. 把当前结点的右子树设置成当前结点右子树的右子树

right = right.right;

  1. 把当前结点的左子树(左子结点)设置成新的结点

left = newNode;

原来的那个“6”因为没有任何结点指向它，所以被系统当作垃圾回收掉了

2. 单旋转—右旋转

1）要求

给你一个数列，创建出对应的平衡二叉树 {10, 12, 8, 9, 7, 6}

2）思路

问题：

当插入“6”时`leftHeight()-rightHeight()>1成立，此时，不再是一颗avl树了

处理过程-进行右旋转

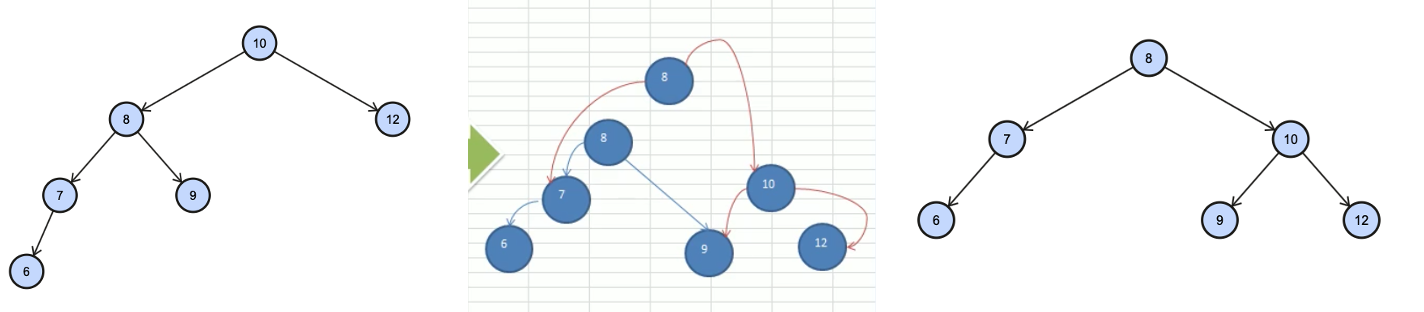
  1. 创建新的结点，以当前根结点的值

Node newNode = new Node(value);

  1. 把新的结点的右子树设置成当前节点的右子树

newNode.right = right;

  1. 把新的结点的左子树设置成带你过去结点的左子树的右子树

newNode.left = left.right;

  1. 把当前结点的值替换成左子结点的值

value = left.value;

  1. 把当前结点的左子树设置成当前结点左子树的左子树

left = left.left;

  1. 把当前结点的右子树(右子结点)设置成新的结点

right = newNode;

原来的那个“8”因为没有任何结点指向它，所以被系统当作垃圾回收掉了

3. 双旋转

1）要求

给你一个数列，创建出对应的平衡二叉树 {10, 11, 7, 6, 8, 9}

2）思路

问题：

当插入“9”时`leftHeight()-rightHeight()>1成立，此时，不再是一颗avl树了

运行结果：

树的高度=4
左子树的高度=1
右子树的高度=3
Root=Node [value=7]

问题分析：

  1. 当符合右旋转的条件时
  2. 如果它的左子树的右子树高度大于它的左子树的高度
  3. 需要先对当前这个结点的左结点进行左旋转
  4. 再对当前结点进行右旋转的操作即可

四、代码实现

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
public class AVLTreeDemo {

	public static void main(String[] args) {
		int[] arr = { 10, 11, 7, 6, 8, 9 };
		AVLTree avlTree = new AVLTree();
		for (int i = 0; i < arr.length; i++) {
			avlTree.add(new Node(arr[i]));
		}
		System.out.println("树的高度=" + avlTree.getRoot().height());//3
		System.out.println("左子树的高度=" + avlTree.getRoot().leftHeight());//2
		System.out.println("右子树的高度=" + avlTree.getRoot().rightHeight());//2
		System.out.println("根结点=" + avlTree.getRoot());//8
		System.out.println("根结点的左子结点=" + avlTree.getRoot().left);//7
	}
}

class AVLTree {
	private Node root;

	public Node getRoot() {
		return root;
	}

	public Node search(int value) {
		if (root == null) {
			return null;
		} else {
			return root.search(value);
		}
	}

	public Node searchParent(int value) {
		if (root == null) {
			return null;
		} else {
			return root.searchParent(value);
		}
	}

	public int delRightTreeMin(Node node) {
		Node target = node;
		while (target.left != null) {
			target = target.left;
		}

		delNode(target.value);
		return target.value;
	}

	public void delNode(int value) {
		if (root == null) {
			return;
		} else {
			Node targetNode = search(value);
			if (targetNode == null) {
				return;
			}
			if (root.left == null && root.right == null) {
				root = null;
				return;
			}
			Node parent = searchParent(value);
			if (targetNode.left == null && targetNode.right == null) {
				if (parent.left != null && parent.left.value == value) {
					parent.left = null;
				} else if (parent.right != null && parent.right.value == value) {
					parent.right = null;
				}
			} else if (targetNode.left != null && targetNode.right != null) {
				int minVal = delRightTreeMin(targetNode.right);
				targetNode.value = minVal;
			} else {
				if (targetNode.left != null) {
					if (parent != null) {
						if (parent.left.value == value) {
							parent.left = targetNode.left;
						} else {
							parent.right = targetNode.left;
						}
					} else {
						root = targetNode.left;
					}
				} else {
					if (parent != null) {
						if (parent.left.value == value) {
							parent.left = targetNode.right;
						} else {
							parent.right = targetNode.right;
						}
					} else {
						root = targetNode.right;
					}
				}
			}
		}
	}

	public void add(Node node) {
		if (root == null) {// 如果是空树，直接让root指向node
			root = node;
		} else {
			root.add(node);
		}
	}

	// 中序遍历
	public void infixOrder() {
		if (root != null) {
			root.infixOrder();
		} else {
			System.out.println("Tree is Empty.");
		}
	}
}

//创建Node节点
class Node {
	int value;
	Node left;
	Node right;

	public Node(int value) {
		this.value = value;
	}

	public int leftHeight() {
		if (left == null) {
			return 0;
		}
		return left.height();
	}

	public int rightHeight() {
		if (right == null) {
			return 0;
		}
		return right.height();
	}

	// return Height of this node
	public int height() {
		return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
		// A ？ B：C ，意思就是如果A为真执行B，否则执行C
	}

	// 左旋转
	private void leftRotate() {
		Node newNode = new Node(value);
		newNode.left = left;
		newNode.right = right.left;
		value = right.value;
		right = right.right;
		left = newNode;
	}

	// 右旋转
	private void rightRotate() {
		Node newNode = new Node(value);
		newNode.right = right;
		newNode.left = left.right;
		value = left.value;
		left = left.left;
		right = newNode;
	}

	/**
	 * 
	 * @param value 希望删除的值
	 * @return 如果找到返回该结点，否则返回null
	 */
	public Node search(int value) {
		if (value == this.value) {
			return this;
		} else if (value < this.value) {
			if (this.left == null) {
				return null;
			}
			return this.left.search(value);
		} else {
			if (this.right == null) {
				return null;
			}
			return this.right.search(value);
		}
	}

	public Node searchParent(int value) {
		if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
			return this;
		} else {
			if (value < this.value && this.left != null) {
				return this.left.searchParent(value);
			} else if (value >= this.value && this.right != null) {
				return this.right.searchParent(value);
			} else {
				return null;
			}
		}

	}

	@Override
	public String toString() {
		return "Node [value=" + value + "]";
	}

	// 添加节点
	public void add(Node node) {
		if (node == null) {
			return;
		}
		if (node.value < this.value) {
			if (this.left == null) {
				this.left = node;
			} else {
				this.left.add(node);// 递归
			}
		} else {
			if (this.right == null) {
				this.right = node;
			} else {
				this.right.add(node);// 递归
			}
		}
		if (rightHeight() - leftHeight() > 1) {
			if (right != null && right.leftHeight() > right.rightHeight()) {
				right.rightRotate();
			}
			leftRotate();
			return;
		}
		if (leftHeight() - rightHeight() > 1) {
			if (left != null && left.rightHeight() > left.leftHeight()) {
				left.leftRotate();
			}
			rightRotate();
		}
	}

	// 中序遍历
	public void infixOrder() {
		if (this.left != null) {
			this.left.infixOrder();
		}
		System.out.println(this);
		if (this.right != null) {
			this.right.infixOrder();
		}
	}
}

运行结果

1
2
3
4
5
树的高度=3
左子树的高度=2
右子树的高度=2
根结点=Node [value=8]
根结点的左子结点=Node [value=7]

参考

  1. 尚硅谷Java数据结构与java算法，韩顺平数据结构与算法 ↩